精密網体積計算 について
近年、レーザー機器による観測で大量の点群が作成され、それに伴い地形もより複雑(正確)に、計測されるようになってきました。
この様な変化に伴い、従来のメッシュ法、平均断面法では捉えきれない地形変化の数量計算に対応すべく、三角網モデルでの精密で 高精度な "精密網体積計算" を用意しました。(TINモデルでできる究極の体積計算です。)

別々の観測網による差分体積計算を、下図のような簡単な2つの地形(観測網)を例にその計算根拠と計算結果を説明します。

地形2D
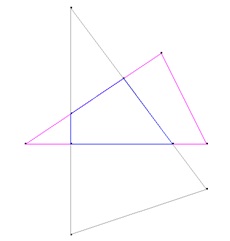
真上から見た2つの地形の位置関係です。
　
地形3D
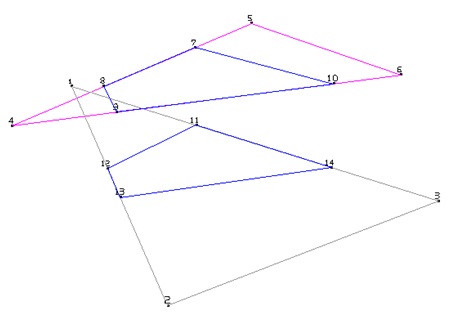
3次元で見た二つの地形の位置関係です。
(青色の部分が共通部分)

各点の座標は以下の通り

番号 x座標 y座標 z座標
1. 30.000 10.000 3.000
2. -20.000 10.000 0.000
3. -10.000 40.000 1.000
番号 x座標 y座標 z座標
4. 0.000 0.000 10.000
5. 20.000 30.000 12.000
6. 0.000 40.000 11.000
番号 x座標 y座標 z座標
7. 14.444444 21.666667 11.444444
8. 6.666667 10.000 10.666667
9. 0.000 10.000 10.25
10. 0.000 32.500 10.8125
番号 x座標 y座標 z座標
11. 14.444444 21.666667 2.222222
12. 6.666667 10.000 1.600
13. 0.000 10.000 1.200
14. 0.000 32.500 1.500

この真ん中の青で囲まれた四角柱の体積を求めます。(7-8-9-10-11-12-13-14)
下図の様に２つの三角柱に分割して考えます。(赤で塗りつぶした部分)
三角柱の体積は水平面積*(各高さの平均) で求めることができます。

各水平面積を求めます
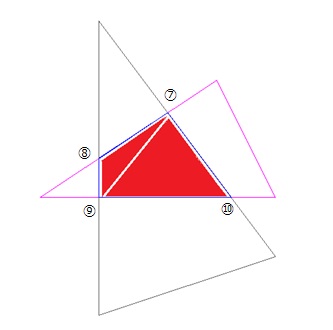
水平面積計算

各線分の水平距離は以下の通り

線分 水平距離
7-8 14.021588
8-9 6.666667
7-9 18.567528
9-10 22.500
7-10 18.055556

3辺の長さを a,b,c とし, s=(a+b+c)/2 とすると
三角形の水平面積は

  ヘロンの公式

で求めることができます。

従って
三角形 7-8-9 の水平面積は 38.888888
三角形 7-10-9 の水平面積は 162.500005
水平面積合計 : 201.388893 となります。


各高さを求めます
高さ計算

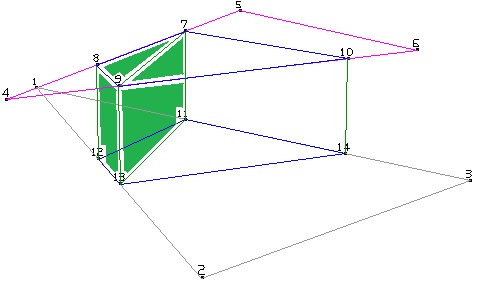
各線分の高さは座標表より

線分 垂直距離
7-11 9.222222
8-12 9.066667
9-13 9.05
10-14 9.3125

各三角柱の体積を求めます

7-9-8-11-13-12 (緑で囲まれた部分) で囲まれた三角柱の体積は
水平面積 (38.888888) * 高さの平均 (9.222222+9.066667+9.05)/3 = 354.393000

7-9-10-11-13-14 (緑で囲まれてない部分) で囲まれた三角柱の体積は
水平面積 (162.500005) * 高さの平均 (9.222222+9.3125+9.05)/3 = 1494.172488

体積合計 354.393 + 1494.172488 = 1848.565488
これが数学で求められる正確な値です。

体積計算

手計算
水平面積 201.388893
体積 1848.565488
LandForms®の精密網体積計算
水平面積 201.389
体積 1848.565

LandForms®の精密網体積計算は、上記の計算を全ての三角網に対して行い、正確に2つのTINモデル地形の差分を計算することができます。

閉じる